Решение уравнения в целых числах
 Недавно закончился прием в заочную математическую школу при Новосибирском государственном университете. Задачи вступительных экзаменов в эту школу, конечно, отражают моду на современные олимпиады.
В этой заметке я рассказываю о моем решении одной из вступительных задач в девятый этой школы. Аналогичная задача для десятого класса предлагается для самостоятельного решения.
 Найдите все пары целых чисел (х; y), удовлетворяющих соотношению Найдите все пары целых чисел (х; y), удовлетворяющих соотношению 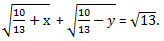
Решение. 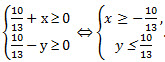 Учитывая, что х и y – целые числа имеем: x ≥ 0 и у ≤ 0. Учитывая, что х и y – целые числа имеем: x ≥ 0 и у ≤ 0.
Если 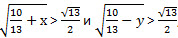 , то , то 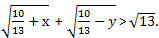 Значит, Значит, 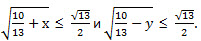
Если 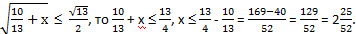 . Значит, 0 ≤ х ≤ 2. . Значит, 0 ≤ х ≤ 2.
При х = 0 имеем 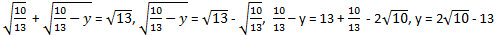 – иррациональное число. Чего быть не может. – иррациональное число. Чего быть не может.
При х = 1 получаем
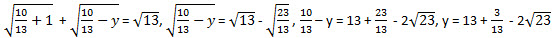 - тоже недопустимое иррациональное число. При х = 2 имеем
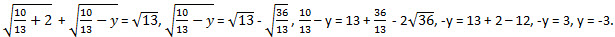 Получили первое решение нашего уравнения – (2; -3). Если 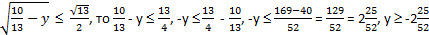 . Значит, -2 ≤ у ≤ 0. При у = -2 получаем 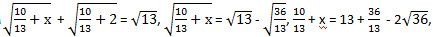 , х = 13 + 2 – 12, х = 3. Получили еще одно решение нашего уравнения – (3; -2). При у = -1 имеем 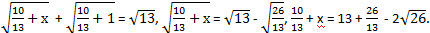 Понятно, что в этом случае х будет иррациональным числом. При у = 0 имеем 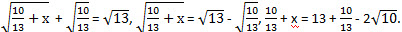 В этом случае х тоже будет иррациональным числом. Итак, имеем два решения: (2; -3) и (3; -2). Ответ: (2; -3), (3; -2). Задача для самостоятельного решения Найдите все пары целых чисел (х; y), удовлетворяющих соотношению Найдите все пары целых чисел (х; y), удовлетворяющих соотношению 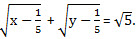 N.B. Идею решения этого уравнения мне подсказал так называемый «принцип Дирихле». В этом принципе говорится, что если суммарное количество предметов (в данном случае √13) нужно разложить по двум ящикам (√13 нужно представить в виде суммы двух неотрицательных слагаемых), то в обоих ящиках не может быть одновременно больше или меньше половины этой суммы (каждое слагаемое не может быть одновременно больше или меньше половины √13 ).
| 
