Решение. Запишем уравнение нашей системы так: х³ = 2 - ху и х³ = 3 - 3ху. Перемножив эти уравнения, получим новое уравнение относительно одной переменной ху.

x³у³ = (2 - ху)(-3 - 3ху),
x³у³ = -6 – 6ху + 3ху + 3х²у².

Пусть ху = t, тогда t³ – 3t² + 3t + 6 = 0.

Конечно, целые корни последнего уравнения можно было бы искать среди делителей свободного члена 6: ±1, ±2, ±3, ±6. Опыт показывать, что такой подход будет неудачным (целых корней у уравнения t³ – 3t² + 3t + 6 = 0 нет).

Легко заметить, что t³ – 3t² + 3t + 6 = (t - 1)³ + 7. Поэтому уравнение t³ – 3t² + 3t + 6 = 0 примет вид

(t - 1)³ + 7 = 0.
(t - 1)³ = -7,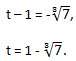

Итак, 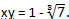Уравнения исходной системы примут вид:

Задача для самостоятельного решения
Решите систему уравнений х³ = 3ху + 3, х³ = ху - 2.
Щелкни здесь и посмотри остальные уроки решения тестов ЕГЭ и ЕНТ!