Решение. Рассмотрим  графическое решение этой задачи.

Вообще говоря, известно, что графиком функции y=5/(x+1) является гипербола. Однако нас интересует только ее правая ветвь, котороя расположена в области [0;+∞). При этом все значения функции y=5/(x+1) будут положительными.

График же функции у = a|x-4| стандартен.

По условию, данное уравнение должно иметь не менее трех корней. Рассмотрим, при каком расположение графиков функций y=5/(x+1) и у = a|x - 4| на координатной плоскости это возможно.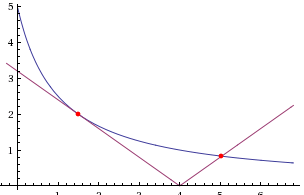
Определим точку касания гиперболы y=5/(x+1) и графика модуля у = a|x-4| как это изображено на рисунке выше.

Прямая у = -ах + 4 будет касаться гиперболы  у = 5/(x+1) только тогда, когда уравнение -а(х - 4) = 5/(x+1) имеет единственное решение.  Рассмотрим решение этого уравнения.

-ах² + 4ах - ах + 4а = 5,

ах² - 3ах - ах - 4а + 5 = 0.

Последнее уравнение имеет единственное решение только тогда, когда его дискриминант равен нулю.

D = 9a² + 4а(4a - 5) = 0,25a² - 20a = 0,a = 0  или а = 0,8.

При а = 0 уравнение -а(х - 4) = 5/(x+1) корней не имеет. а = 0,8 удовлетворяет нашему требованию (проверьте самостоятельно!). Случай а = 0,8 изображен на рисунке выше.

Правая ветвь модуля пересекает ветвь гиперболы всегда в одной точке.

При a > 0,8 левая ветвь графика функции  у = a|x-4| будет пересекать ветвь гиперболы в двух точках до тех пор, пока прямая у = -а(х - 4) будет пересекать ось ординат в точке ниже 5.

Прямая у = -а(х - 4) пересекает ось ординат при х = 0 и у = 4а. 

Значит, 4а < 5< a < 1,25.

Поэтому условию данной задачи удовлетворяют все значения а из промежутка (0,8; 1,25).

Ответ: (0,8; 1,25).