Логарифмическое неравенство
 Как известно, решение задании типа С требует наличие у учащихся глубоких знаний. Это, как правило, задания повышенного и высокого уровня сложности, которые не рассчитаны на массового школьника, даже если он является отличником. О решении одного из таких неравенств рассказывается в этой заметке.
Официально считается, что задания ЕГЭ не выходят за рамки школьной программы. Однако далеко не все выпускники средних школ знакомы с формулировками некоторых заданий типа С, не говоря уже о методах решения таких заданий.
Как правило, задания типа С нацелены на проверку знаний и умений выпускников спецкшол или профильных классов, участников предметных олимпиад и т. д. Эксперты считают, что ЕГЭ должен включать в себя подобные сложные задания, чтобы иметь возможность различать учеников при поступлении в вузы с высокими требованиями к уровню подготовки.
Опять кто-то кого-то должен различать. Как будто мы имеем дело с баранами среди которых нужно выбрать наиболее породистых. А может быть имеет смысл самим ученикам предоставить возможность показать, что они могут претендовать на места в вузы с высокой математической подготовкой. Для этого каждый из таких претендентов должен пройти дополнительный конкурсный отбор в эти вузы.
Так или не так покажет будущее. Однако всегда будут задания для всех выпускников и для элиты в хорошем смысле этого слова, для тех кто годы учебы потратил на учебу, а не на бесполезную тусовку. Для таких трудяг и посвящена эта статья.
Решение. Понятно, что это задание не "для всех". Чтобы его решить нужны "особые" знания и умения. вот их то мы здесь и продемонстрируем.
Найдем сначала ОДЗ. х4 - 18x² + 82 = (x² - 9)² + 1) > 0 при любом х.
6 - х - х² = 0. Предлагаем читателям самостоятельно решить уравнения 6 - х - х² = 0 при помощи инструмента "Онлайн калькулятор" из меню "Инструменты" и получить корни этого уравнения х = 2 и х = -3.
6 - х - х² ≥ 0 при х ∈ [-3; 2]. Значит, ОДЗ задается промежутком [-3; 2].
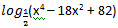 = log½((x² - 9)² + 1) <= 0. Равенство log½((x² - 9)² + 1) = 0 не имеет место, так как 3 ∉ [-3; 2], а х = -3 не удовлетворяет данному неравенству.
Значит, промежуток (-3; 2] является решением данного неравенства. | 
Решите неравенство
.
