Иррациональное неравенство типа С3
Как известно правильное решение задания типа С3 в тестах ЕГЭ оценивается в три балла. Поэтому решение таких заданий повышает шансы абитуриента при поступлении в вуз. В этой заметке рассматривается авторское решение из подготовительного теста ЕГЭ-2012.
Решение. Найдем ОДЗ. 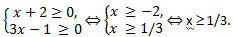
Пусть 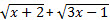 = а, тогда а2 = x + 2 + 2 = а, тогда а2 = x + 2 + 2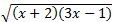 + 3x - 1; а2 = 4x + 1 + 2 + 3x - 1; а2 = 4x + 1 + 2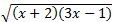 ; ; 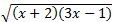 = (а2 - 4x - 1)/2. Поэтому данное неравенство примет вид = (а2 - 4x - 1)/2. Поэтому данное неравенство примет вид
(а2 - 4x - 1)/2 ≤ 1 – 2x + а; а2 - 4x - 1 ≤ 2 – 4x + 2а; а2 - 2a - 3 ≤ 0. Разложив левую часть последнего неравенства на множители получим
(а + 1)(а - 3) ≤ 0. Значит, -1 ≤ а ≤ 3.
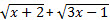 = 3, = 3,x + 2 + 2 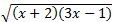 + 3x - 1 = 9, + 3x - 1 = 9, 2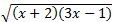 = 8 - 4x, = 8 - 4x, 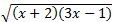 = 4 - 2x, = 4 - 2x,(x + 2)(3x - 1) = 16 - 16x + 4x², 3x² + 5x - 2 = 16 - 16x + 4x², x² - 21x + 18 = 0. Чтобы сократить время далее я воспользуюсь страницей с инструментом "Решение квадратного уравнения", которое можно получить из меню справа "Инструменты". Нетрудно подсчитать, что x1 - посторонний корень, так как при х = x1 4 - 2х < 0. х = x2 является корнем решаемого уравнения, так как все переходы, осуществляемые при его решении будут равносильными. Значит, ответом нашей задачи будет промежуток [1/3; x2].
Задача для самостоятельного решения
 Решите неравенство Решите неравенство 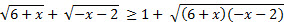 . . | 
