Задача на отношение площадей трапеции (типа С4)
Самыми трудными на ЕГЭ по математике считаются задачи типа С. Поэтому продолжаем публикацию решений этих задач. В этой статье рассматривается решение уже известной задачи. Однако ее решение осуществляется в общем виде. Такой подход позволяет экономить время и силы учащихся на экзамене.
C4.Основания трапеции равны a и b. Прямая, параллельная основаниям, разбивает трапецию на две трапеции, площади которых относятся как 2: 3. Найти длину отрезка этой прямой, заключенного внутри трапеции.
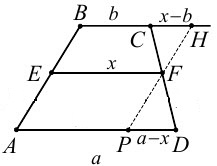 Решение. Неизвестно как относятся площади трапеций BCFE и AEFD - как 2:3 или как 3:2. Поэтому эту задачу будем решать в общем виде. Решение. Неизвестно как относятся площади трапеций BCFE и AEFD - как 2:3 или как 3:2. Поэтому эту задачу будем решать в общем виде.
Обозначим искомый отрезок ЕF через х. Пусть площади трапеций BCFE и AEFD относятся как m:n.
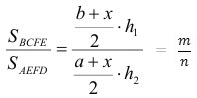 . Отсюда . Отсюда 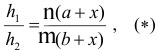
где h1 и h2 - высоты этих трапеций.
Через точку F проведем отрезок РН параллельно АВ (можно было бы этот отрезок провести через точку С или D). Тогда треугольники PFD и CHF подобны (докажите самостоятельно) и 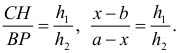
Испольуем соотношение (*):
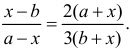
Решая полученное уравнение относительно переменной х, получаем m(х² - b²) = n(a² - x²), (m + n)x² = na² + mb²,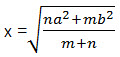 . .
Если площади трапеций BCFE и AEFD относятся как 2:3, то m = 2, n = 3 и искомый ответ будет 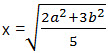 . .
Если же площади трапеций BCFE и AEFD относятся как 3:2, то m = 3, n = 2 и искомый ответ будет 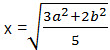 . .
Ответ: 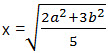 или или 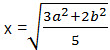 . . | 
