Такие задачи обычно не входят в программу общеобразовательной школы. Поэтому их решение необходимо дополнительно освещать в соответствующей методической литературе и обсуждать на Интернет-площадках
Поэтому я в своей рассылке "Математика. Подготовка к ЕГЭ и ЕНТ" (http://content.mail.ru/cgi-bin/counter?27136+3) опубликовал решение одной из таких задачи из сборника для подготовки учащихся к ЕГЭ-2012 по математике.
Найти все значения а, при каждом из которых функция f(x) = x2 - ∣x - a2∣ - 5x имеет хотя бы одну точку максимума.Решение.
Раскроем модуль:
При x ≤ a
2: f(x) = х
2 - 4x - a
2,
при x > a
2: f(x) = х
2 - 6x + a
2.
Графиком функции f(x) при х ≤ a
2 является часть параболы. Вершина этой параболы имеет абсциссу 2. Точно также графиком функции f(x) при х > a
2 является часть параболы, у которой вершина имеет абсциссу 3.
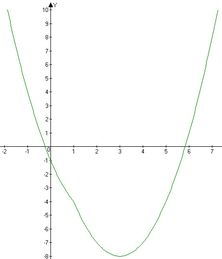
Если a
2 ≤ 2, то график функции f(x) имеет вид рисунка выше этих строк. Понятно, что в этом случае никаких точек экстремума нет, значит, нет и точек максимума.
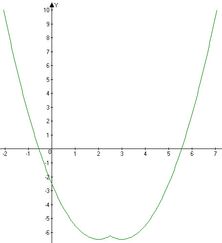
Если 2 < a
2 < 3, то график функции f(x) приведен на втором рисунке. В этом случае точкой максимуму является х = 2. Решив неравенство 2 < a
2 < 3 получим искомые значения параметра а.
2 < a
2 < 3, √2 < ∣a∣ < √3, a ∈ (-√3; -√2) ∪ (√2; √3).
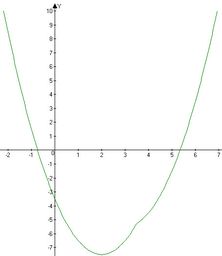
Если a
2 ≥ 2, то график функции f(x) имеет вид последнего рисунка. Очевидно, что и в этом случае никаких точек экстремума нет.
Очередной раз возникает вопрос: "Где взять аналогичные задачи для работы с учащимися?". Конечно, можно скачать много подготовительных вариантов и таким образом накопить соответствующий материал.
Однако еще советской методики математики П.М. Эрдниев предлагал учащимся (а, значит, и учителям) учиться составлять такие задачи самим. Не буду распространяться о полезности таких упражнений. Думаю, что это высший пилотаж в работе учителя и ученика. Но как составить упражнений аналогичные рассмотренному выше?
Ответ: a ∈ (-√3; -√2) ∪ (√2; √3).
На ЕГЭ по математике в разделе С очень часто предлагаются уравнения, неравенства или их системы с параметрами на нахождение значений этого параметра, при которых выполняется то или иное условие.
