Область определения функции в Wolfram|Alpha
 Как правило, на экзамене ЕНТ (аналог ЕГЭ в Казахстане) в каждом варианте содержится задание на вычисление области определения функции. Такие задания удобно решать при помощи сервиса Wolfram|Alpha.
Для вычисления области определения функции в Wolfram|Alpha есть правило (формат) запроса
domain f(x)
где domain буквально переводится как "область определения функции", а f(x) - это та функция, область определения которой вам необходимо вычислить. По такому формату запроса система Wolfram|Alpha выводит пользователю: область определения функции в терминах теории множеств, ее графическую иллюстрацию и схематическое изображение графика функции. Этого вполне достаточно, чтобы получить правильный ответ на соответствующее тестовое задание и сверить его с ответами для выбора.
Вот и вся небольшая теория по теме "область определения функции". А теперь перейдем к конкретной практике и рассмотрим несколько примеров на вычисление области определения функций при помощи системы Wolfram|Alpha. Отметим лишь, что все эти задания взяты мной из сборника для подготовки ЕГЭ по математике 2012 года без соответствующих пяти ответов для выбора правильного среди них.
1. Найдите область определения функции у = 1/(x² + x).
Сначала перейдем на главную страницу сервиса Wolfram|Alpha по адресу http://www.wolframalpha.com/ и введем запрос в виде domain 1/(x^2+x) . На следующем рисунке указано как следует вводить наш запрос и получить на него ответ.
После указания "получить ответ" (нажатия на кнопку "=") мы получить следующий искомый результат.
Понятно, что это простое задание можно было достаточно быстро решить устно, не прибегая к помощи Wolfram|Alpha. Его мы рассмотрели для того,чтобы объяснить технику работы по вычислению области определения и множества значений функции в системе Wolfram|Alpha.
Теперь рассмотрим решение более сложного задания.2. Найдите область определения функции: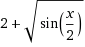 ."Переведем" это задание на язык понятный системе Wolfram|Alpha: domain 2+sqrt(sin(x/2)). Выполним процедуру получения ответа как и в предыдущем примере.
Этот ответ однозначно соответствует правильному ответу, который содержится в сборнике тестов, откуда был заимствован этот пример. 3. Найдите область определения функции:  .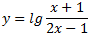
Как видно из рисунка система Wolfram|Alpha дала хотя и правильный,но не очень корректный ответ: х < -1 или 2х > 1. Это, как говорится издержки системы. Вообще, на Wolfram|Alpha надейся, но сам не плошай! Вот пример, решение которого в системе Wolfram|Alpha никак не соответствует ответам из сборника тестов для подготовки к ЕНТ 2012 года. 4. Найдите область определения функции у =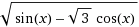 
Запись данной функции в системе Wolfram|Alpha имеет вид domain sqrt(sin(x)-sqrt(3)cos(x)). Полученное решение представлено на следующем рисунке.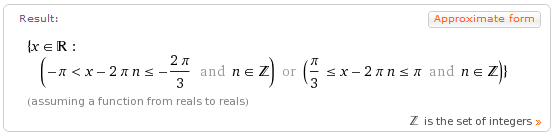 
Это решение не совпадает ни с одним из ответов для выбора правильного из них в соответствующем тестовом задании. Поэтому следует помнить, что система Wolfram|Alpha иногда дает и сбои. Задания для самостоятельного решения1. Найдите область определения функции: у = 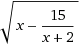 . 2. Найдите область определения функции: у = 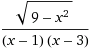 3. Найдите область определения функции: 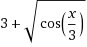 . 4. Найдите область определения функции: 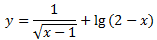 . 5. Найдите область определения функции: у = log 2(x + 6) + log 3(6 - x). 6. Найдите область определения функции:  . |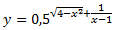 
