Как известно, задачи типа С4 экзамена ЕГЭ не очень трудные. Однако при их решении учащихся поджидают не математические, а логические, а если быть еще точнее психологические стереотипы, которые невольно наталкивают их на совершение ошибок. Отметим, что такие ошибки совершают большинство выпускников средних школ, так как они не привыкли решать такого типа задач, да и в школьных учебниках геометрии такие задачи практически отсутствуют.

Поэтому сборники для подготовки учащихся к сдаче ЕГЭ по математике в этом плане представляют собой бесценный методический материал для плодотворной работы школьного учителя. Как бы ни развивалась эволюция ЕГЭ, по моему мнению, эти материалы будут всегда сохранять свою педагогическую актуальность.

Однако вернемся к "нашим баранам" и рассмотрим пример одной из таких задач, которая может стать камнем преткновения на ЕГЭ по математике для учащихся.

C4 Боковые стороны KL и MN трапеции KLMN равны 8 и 17 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 17,5. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM..

Решение.
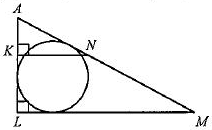
В каждой трапеции отрезок, соединяющий середины диагоналей равен полу разности оснований, а средняя линя - полусумме оснований.

 Пусть а и b - основания данной трапеции, тогда

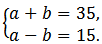
Решив эту систему получаем а = 25, b = 10. Значит, LM = 25, KN = 10.

 Так  как стороны LM и KN треугольников ALM и AKN параллельны, то эти треугольники подобны. При этом коэффициент подобия равен 25/10 = 2,5.

AL = 2,5AK,
AK + KL = 2,5AK,
AK + 8 = 2,5AK,1,5AK = 8,
AK= 16/3. Значит, AL = AK + KL = 16/3 + 8 = 40/3.

AM = 2,5AN,
AN + NM = 2,5AN,
 AN + 17 = 2,5AN,
1,5AN = 17,
AN = 34/3. AM = AM + NM = 34/3 + 17 = 85/3.

Так как AL² = LM² + AM²,  то треугольник ALM - прямоугольный.

В прямоугольном треугольнике радиус вписанной окружности находится по формуле r = (a + b - c)/2. Поэтому r = (40/3 + 25 - 85/3)/2 =  5. 

Казалось бы задача решена и пора на ней ставить точку. Однако здесь многих ожидает ловушка. Дело в том, что чертеж может быть другим.