О решении задачи С5 ЕГЭ-2014 при помощи графиков

В сообщении ЗАДАЧА С5 ЕГЭ-2014 по адресу http://www.liveinternet.ru/users/kifar/post329198627/ я рассказывал о решении такой задачи ЕГЭ-2014 по математике

C5. Найдите все значения параметра a , при которых уравнение (|x - 2| + |x + a|)² - 7(|x - 2| + |x + a|) - 4a(7 - 4a) = 0 имеет ровно два решения.

Уравнение (|x - 2| + |x + a|)² - 7(|x - 2| + |x + a|) - 4a(7 - 4a) = 0 в свою очередь разбивается на совокупность двух уравнений |x - 2| + |x + a| = 4а и |x - 2| + |x + a| = 7 - 4а.

Я знаю несколько подходов к решению этой совокупности. Здесь я рассмотрю только два подхода, которые связаны с построением графиков уравнений.

Первый подход. Сервис WolframAlpha (http://www.wolframalpha.com/) Для решения, а точнее построения графиков уравнений нашей совокупности надо дать системе WolframAlpha команду

plot (|x - 2| + |x + a| = 4a, |x - 2| + |x + a| = 7 - 4a) for x=-10..10, a=-10..10

В результате нам будет выдана следующая картинка

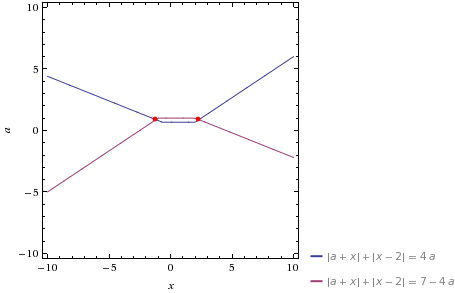
По этой картинке очень трудно проанализировать построенный график. Однако этот рисунок позволяет наметить план решения нашей задачи. На этом эвристическая роль системы WolframAlpha заканчивается, так как понятно, что построить график нашей совокупности можно и "в ручную". Об этом рассказано в ролике из сообщения моего блога  ЗАДАЧА С5 ЕГЭ-2014 по адресу http://www.liveinternet.ru/users/kifar/post329198627/.

Таким образом, сервис WolframAlpha использован здесь мною только как эвристическое средство, наводящее на строгое математическое решение задачи С5 ЕГЭ-2014.

Второй подход Совокупность уравнений |x - 2| + |x + a| = 4а и |x - 2| + |x + a| = 7 - 4а перепишем тек: |x - 2| = 4а - |x + a| и |x - 2| = 7 - 4а - |x + a|. Построим графики трех функций y = |x - 2|, y = 4а - |x + a| и  y = 7 - 4а - |x + a|.

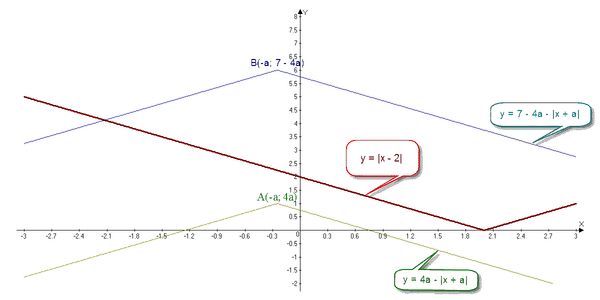
График  функции y = |x - 2| неподвижен, а графики углов y = 4а - |x + a| и  y = 7 - 4а - |x + a| подвижны.При этом их вершины лежат на прямых y = -4x и y = 7 + 4x соответственно.

Это наблюдение позволяет реализовать следующую "простую" идею для решения нашей задачи. Совокупность рассматриваемых уравнений имеет ровно два решения а трех случаях:

1) Вершина угла y = 4а - |x + a|, т. е точка А(-а; 4a) расположена внутри прямого угла y = |x - 2|, в вершина угла y = 7 - 4а - |x + a|, т.е. точка В(-а; 7 - 4a) расположена вне этого угла. При этом точки А и В не могут лежать на сторонах угла y = |x - 2|, так ка в этом случае система будет иметь бесконечное множество решений.

2) Точки А и В поменяются местами (как на рисунке сверху).

3) Точки А и В расположены внутри прямого угла y = |x - 2| и совпадают, т. е. 4a = 7 - 4а. При этом надо проверить, чтобы совпавшие точки А и В лежали внутри угла y = |x - 2|.

Для каждого случая можно составить несколько алгебраических моделей. Самой простой, на мой взгляд, является модель, которая учитывает условие расположения вершин А и В на прямых y = -4x и y = 7 + 4x. В этом случае, например пункт 1) нашего плана будет реализован системой из двух простейших линейных неравенств.

Хотите овладеть искусством и наукой решения тестов ЕГЭ и ЕНТ - посетите и подпишитесь на мой видеоблог на Youtube!