Задание типа С6 о коробках
 Имеются 25 коробок, массой 13 кг каждая и 19 коробок, массой по 29 кг каждая. Все эти коробки раскладываются по двум контейнерам. Пусть S – модуль разности суммарной массы коробок в контейнерах. Найдите наименьшее значение S, если
a) дополнительно требуется, чтобы в контейнерах находилось одинаковое количество коробок.б) без дополнительного условия п.а)Решение. Пусть в первом контейнере находится x коробок массой 13 кг и y коробок массой 29 кг. Тогда во втором контейнере будет находится соответственно по 25 - x и по 19 - y коробок. Поэтому модуль разности суммарной массы можно записать: S=|13x + 29y - ((25 - x)⋅13 + (19 - y)⋅29)| или S=2⋅|13x + 29y - 438|. a) Условие равенства количества коробок выражается в виде равенства x + y = (25 - x) + (19 - y), 2x + 2y = 44, x + y = 22. Тогда выражение для модуля разности суммарной массы коробок в контейнерах запишется S=2⋅|13x + 638 - 29x - 438|=16⋅|25 - 2x|. Поскольку S ∈ Z, то минимальное значение выражения |25 - 2x| может быть сделано равным только единице, поэтому ответ на п.а) равен 16 .Этот результат достигается при x= 12 или x=13. б) Минимальное значение выражения S=2⋅|13x + 29y - 438| равно 0. Чтобы узнать при каких значениях х и у это значение достигается нужно решить уравнение 13x + 29y = 438 в целых числах. 13x = 438 - 29y, 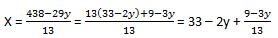 (1) Так как х - целое число, то 9 - 3y = 13k, где k - целое число. 13k + 3y = 9, 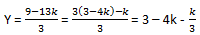 (2) В силу того, что у тоже целое число, то k = 3t.
Из (2) следует, что у = 3 - 4 ⋅ 3k + k, y = 3 - 13k.
Из (1) получаем, что x = 33 - 2(3 - 13k) + 13 ⋅ 3t = 27 + 29t.
Итак, x = 27 + 9t, у = 3 - 13k.
Чтобы проверить правильность найденного нами решения введем в окошко для заданий системы wolframalpha.com следующее указание "solve 13x + 29y = 438 in integers" (без кавычек) и нажмем на кнопку "получить ответ".
Так как 0 ≤ х ≤ 9, то 0 ≤ 27 + 29t ≤ 9, -27 ≤ 29t ≤ -2, 0 ≤ x 0.
Последнее неравенство не имеет решений в целых числах. Значит, уравнение 13x + 29y = 438 не имеет решений в целых числах, для х ∈ [0; 25]. Поэтому S не может принимать значение 0. Поскольку S четное число, наименьшее значение S может быть равно 2. Для этого найдет решение уравнения 13x + 29y - 438 = ±1.
Уравнение 13x + 29y = 438 + 1, 13x + 29y = 439 имеет решение х = 7 и у = 12 (решити самостоятельно по предыдущему образцу или при помощи системы wolframalpha.com). Значит, минимальная разность масс контейнеров будет равна 2.
Ответ: а) 16, б) 2.
Задачи для самостоятельного решения
1. Имеется 33 коробки массой 19 кг каждая и 27 коробок массой 49 кг каждая. Все эти коробки раскладывают по двум контейнерам. Пусть S - модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S:a)если дополнительно требуется, что в контейнерах должно находится одинаковое количество коробок; b)без дополнительного условия пунка a.
2.Имеется 17 коробок массой 37 кг и 25 коробок массой 61 кг каждая. Все эти коробки раскладывают по двум контейнерам. Пусть S - модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S: a)если дополнительно требуется, что в контейнерах должно находится одинаковое количество коробок; b)без дополнительного условия пункта a.
3.Имеется 27 коробок массой 17 кг и 19 коробок массой 61 кг каждая. Все эти коробки раскладывают по двум контейнерам.Пусть S - модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S: a)если дополнительно требуется, что в контейнерах должно находится одинаковое количество коробок; b)без дополнительного условия пункта a.
4.Имеется 25 коробок массой 31 кг и 15 коробок массой 51 кг каждая. Все эти коробки раскладывают по двум контейнерам. Пусть S - модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S: a)если дополнительно требуется, что в контейнерах должно находится одинаковое количество коробок; b)без дополнительного условия пункта a. | 
