Метод оценки в тестах ЕНТ
Как известно, на решение каждого тестового задания ЕНТ отводится не более 1,5 минуты. За это время весьма трудно решить даже простое задание типа:
 Избавиться от иррациональности в знаменателе 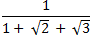 . А) 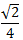 B) 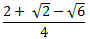 C) 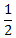 D) 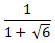 E) 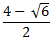
Для того чтобы это задание выполнить за вполне приемлимое время (не более 1 минуты) рассмотрим следующий прием.
Прежде всего вычислим на своем личном калькуляторе или на, этом онлайн калькуляторе что √2 ≈ 1,4...; √3 ≈ 1,7...; √5 ≈ 2,2...; √6 ≈ 2,4...; √7 ≈ 2,6... . Затем запишите в тетради и добросовестно вызубрите эти приближенные значения. Постарайтесь обязательно вызубрить приближенные значения указанных выше радикалов, так как на экзамене у вас не будет времени их вспоминать и тем более заново выводить. Поэтому зубрежка в данном случае непременно вам поможет - позволит сейчас и в будущем быстро и правильно решать подобные тестовые задания ЕНТ. Вот основная идея дальнейшего решения. Найдем сначала приближенной значение данного иррационального выражения. Затем, сравнив найденное значение со значениями предложенных для выбора ответов, отбросим все неверные решения, кроме одного, которое придется считать верным.
Легко подсчитать что 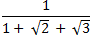 ≈ 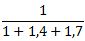 ≈ 0,2. Выпишем в тетради (или на черновике) все номера ответов:
Прежде всего обратим внимание, что ответ D) не может быть правильным (он содержит иррациональность в знаменателе). Зачеркнем его: a b c d e
Теперь проверим все ответы на выполнение условия: быть значительно больше или меньше 0,2.
Так как √2/4 ≈ 1,4/4 > 0,3 и 1/2 > 0,5, то имеем
a b cd eКроме этого 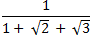 ≈ (4 - 2,4) : 2 = 1,6 : 2 = 0,8 > 0,2, то ≈ (4 - 2,4) : 2 = 1,6 : 2 = 0,8 > 0,2, то a b cdeИз пяти ответов четыре оказались неверными, поэтому правильный ответ B).
При должном старании и соответствующей практике можно добиться выполнения таких заданий за время не более одной минуты - к чему мы и стремились. Р.М. Салимжанов Другие уроки решения тестов ЕНТ читайте здесь | 
