Площадь треугольника (задание типа С4)
 Дан треугольник ABC со сторонами АВ = 34, AC = 65 и BC = 93. На стороне ВС взята точка М, причём AM = 20. Найдите площадь треугольника АМВ. Дан треугольник ABC со сторонами АВ = 34, AC = 65 и BC = 93. На стороне ВС взята точка М, причём AM = 20. Найдите площадь треугольника АМВ.
Как правило, после чтения условия задачи следует внимательно проанализировать его. Для этого многие механически читают условие задачи по нескольку раз или пытаются пересказать его своими словами. Конечно же этакие деяния никоим образом не приведут к пониманию о чет говорится в условии задачи и что требуется найти. Как осуществлять правильный изучение условия задачи вообще покажу на примере этого конкретного тестового задания типа С4.
Числа 34, 65 и 93 - стороны данного треугольника. А существует ли такой треугольник? Сначала (см. рисунок ниже) построим отрезок ВС длиной 93 (это самая большая сторона треугольника), а затем две окружности с центрами в точках В и С и радиусами 34 и 65 соответственно. Эти окружности будут пересекаться в точке А, лежащей не на отрезке ВС, так как 34 + 65 > 93. Значит искомый треугольник существует.
Конечно, эти построения выполнять в реалии не стоит, но провести такие мыслительные эксперименты весьма полезны для понимания условия задачи.
Как узнать где находится точка М? Да весьма просто - построить окружность с центром в точке А и радиусом 20 (20 - длина АМ). Если эта окружность не пересечется с прямой ВС, то такой точки М на ВС нет и задача не имеет решения. Если эта окружность только коснется прямой ВС, то задача имеет единственное решение и если окружность пересечет ВС в двух точках, то надо искать два решения нашей задачи.
Если радиус окружности будет достаточно большим, то весь отрезок ВС будет лежать внутри соответствующего круга и наша задача не будет иметь решений.
Таким образом, количество решений задачи зависит от расстояния от точки А до прямой ВС, т. е. от высоты АН треугольник АВС.
После такого анализа условия задачи легко получить следующее решений этой задачи.
Решение I.
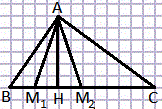 Точка М может распологать левее высоты АН и правее этой высота, то есть иметь два положения М1 и М2 (если только М не совпадает с Н и АМ > АН).Поэтому сначала вычислим длину высоты АН треугольника АВС. Точка М может распологать левее высоты АН и правее этой высота, то есть иметь два положения М1 и М2 (если только М не совпадает с Н и АМ > АН).Поэтому сначала вычислим длину высоты АН треугольника АВС.
SΔАВС = 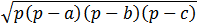 , где р, а, b, с - полупериметр и стороны треугольника АВС соответственно (формула Герона). р = 0,5(34 + 65 + 93) = 96, SΔАВС = , где р, а, b, с - полупериметр и стороны треугольника АВС соответственно (формула Герона). р = 0,5(34 + 65 + 93) = 96, SΔАВС = 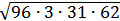 = 744. = 744.
Площадь треугольника АВС можно вычислить по формуле SΔАВС = 0,5ВС ⋅ АН. Откуда АН = 2SΔАВС/BC = 2 ⋅ 744/93 = 16. Так как АМ = 20, то АМ > АН и точка М имеет два различных расположения на чертеже. При этом ВН = 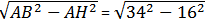 = 30. = 30.
Для вычисления площади треугольника АМВ (АМ1В и АМ2В) найдем ВМ1 и ВМ2.
М1Н = 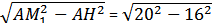 = 12, ВМ1 = ВН - М1 = 30 - 12 = 18. SΔАМ1В = 0,5BМ1⋅AH = 144. = 12, ВМ1 = ВН - М1 = 30 - 12 = 18. SΔАМ1В = 0,5BМ1⋅AH = 144.
Так как М2Н = М1Н = 12, то ВМ2 = 30 + 12 = 42. SΔАМ2В = 0,5BМ2⋅AH = 336.
Ответ: 144 или 336.
При решении этой задачи очень легко упустить из виду тот момент, что точка М может лежать как правее, так и левее точки Н. Такое возможно, например, если на осуществлять серьезного и вдумчивого анализа условия задачи.
Однако есть такой метод решения этой задачи, который обязательно приведет к тому, что у точки М есть два возможных расположения на чертеже. Этот метод называется координатным методом.
Решение II.
Введем систему прямоугольных координат так, как это сделано на следующем рисунке.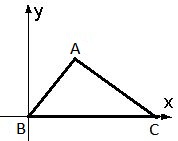 Очевидно, что точка С имеет координаты (93; 0). Координаты точки А(x; y) найдем из решения системы Очевидно, что точка С имеет координаты (93; 0). Координаты точки А(x; y) найдем из решения системы 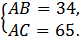
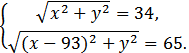
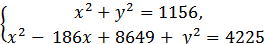
1156 - 186x + 8649 = 4225,
-182x = -5580,
x = 30.
Так как х2 + y2 = 1156, то y2 = 1156 - 900, y2 = 256, y1 = 16, 2 = -16. Так как точка А лежит в первой четверти, то y = 16. Значит, точка А имеет координаты (30; 16). При этом 16 - высота треугольника АВС.
Так как АМ = 20, то точка М лежит на окружности с центром в точке А и радиусом 20 и на прямой ВС (y = 0). Поэтому координаты точки М являются решением систему уравнений 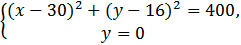
(х - 30)2 + 256 = 400, (х - 30)2 = 144, х - 30 = -12 или х - 30 = 12.
х = 18 или х = 42. Значит точка М имеет координаты (18; 0) или (42; 0).
У треугольника АМВ высота равна 16, а основание может быть 18 или 42. Значит площадь треугольника АМВ равна 0,5⋅18⋅16 = 144 или 0,5⋅42⋅16 = 336.
Ответ: 144 или 336.
Ценность второго решения состоит в том, что мы на задумывались о том, что точка М может иметь два расположения. За нас "думали" уравнения.
Не следует думать, что это все возможные решения нашей задачи. Рассмотрим еще одно решений, если быть точнее только его план.>
Решение III.
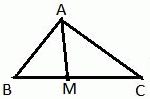 Рассмотрим треугольник АМВ. Рассмотрим треугольник АМВ.
Сначала вычислим величину угла В из треугольника АВС по теореме косинусов.
Затем применим теорему косинусов для стороны АМ треугольника АМВ. АМ2Н = ... .
Из полученного квадратного уравнения относительно АМ найдем два значения АМ.
Зная cos∠В вычислим sin∠B.
Площадь треугольника АМВ найдем по формуле S = 0,5АВ⋅АМbsin∠B.
Реализовать на практике план этого решения предоставляю читателям самостоятельно.
Задача для самостоятельного решения
Дан треугольник ABC со сторонами АВ = 17, AC = 25 и BC = 28. На стороне ВС взята точка М, причём AM = 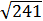 . Найдите площадь треугольника АМВ. |

