Система WolframAlpha и арифметические задачи тестов ЕГЭ и ЕНТ (часть I)
Система WolframAlpha, автором которой является британский ученный Stephen Wolfram прекрасное средство для решения арифметических задач тестов ЕГЭ и ЕНТ по математике. Основные приемы решения таких задач рассматриваются в этой статье.
При решении многих задач тестов ЕГЭ и ЕНТ по математике возникает насущная потребность в проверке полученных учеником ответов. Однако чаще всего хотелось бы посмотреть правильный ход решения той или иной задачи. Конечно, есть ответы к задачам во многих сборниках тестов для подготовки к ЕГЭ и ЕНТ. Однако там как правило нет образцовых решений изучая которые можно научиться решать аналогичные задания.
Учиться решать задачи ЕГЭ и ЕНТ по математике можно и на примерах решения имеющихся в сборниках стандартных задач. Можно, конечно, это делать с учителем или репетитором. Чаще всего это это делать учеником самостоятельно. Для этого существуют различные вспомогательные средства решения. Одним из таких средств является англоязычная система WolframAlpha ( http://www.wolframalpha.com) и русскоязычная система Нигма ( http://nigma.ru/index.php?t=math&).
В этой и других моих статьях будут раскрыты основные приемы решения задач тестов ЕГЭ и ЕНТ по математике при помощи системы WolframAlpha ( http://www.wolframalpha.com).
I. Основные арифметические операции и функции
Сложение: a+b Вычитание: a-b Умножение: a*b Деление: a/b Возведение в степень: a^b Извлечение корня: Sqrt[x] либо (х)^1/2 либо : x^(1/n) Модуль числа:abs(х)
Десятичная запись числа -18,341 в системе WolframAlpha будет выглядеть: -18.341 .
Даже этих скудных знаний о системе WolframAlpha вполне достаточно для решения арифметических заданий тестов ЕГЭ и ЕНТ (особенно ЕНТ) по математике.
Пример 1. Выполните действия: 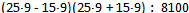 .
Самое главное - это правильно записать данной выражение в системе обозначений сервиса WolframAlpha. В данном случае это можно сделать так: 0.25^(1/2)+(0.81^0.5)*(100^0.5). Возможно, что в этой записи есть лишние круглые скобки. Однако это снижает риск того, что наша запись будет неправильно понята системой WolframAlpha. Затем следует вызвать систему WolframAlpha по адресу http://www.wolframalpha.com или воспользоваться окошком для ввода этого выражения ниже.
После подстановки выражения 0.25^(1/2)+(0.81^0.5)*(100^0.5) в окошко ввода задания для системы WolframAlpha и нажатия клавиши Enter или кнопку "=" практически мгновенно получим ответ 9.5.
Пример 2. Вычислите: 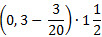 .
Сначала запишем указанное в задание арифметическое выражение в форме понятной для системы WolframAlpha. Это можно сделать различными способами, например, так: (0.3 - 3/20)*1.5 или (0/3 - 3/20)*(3/2) и. т. п..
В окошко ввода данных следует ввести, например, выражение (0.3 - 3/20)*1.5 и нажать на клавишу Enter или кнопку "=" в этом же окошке. Попытайтесь это сделать самостоятельно.
В результате вы получите ответы в виде десятичных дробей (0,225 и 0,2250) и в виде обыкновенной дроби 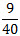 . Пример 3. Найдите значение выражения: 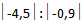
Главное правильно перевести перевести это задание на "язык" системы WolframAlpha. Это можно сделать так: abs(-4.5)/abs(-0.9). После передачи этого задания системе WolframAlpha нам остается только лицезреть полученный ответ 9.
Однако не всякое задание будет нам решать система WolframAlpha. Вот один из таких примеров. Пример 4. Освободиться от иррациональности в знаменателе: 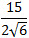 . Это задание легко решается и без системы WolframAlpha, но проверить правильность полученного ответ хотелось бы. Передав системе WolframAlpha в виде 15/(2*sqrt(6)) мы не получим ожидаемого получим ответа.
Рассмотрим теперь еще несколько интересных заданий.
Пример 5. Найдите значение выражения 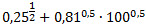 . Запишем данное выражение в системе обозначений сервиса WolframAlpha так 0.25^(1/2)+(0.81^0.5)*(100^0.5). Возможно, что в этой записи есть лишние скобки. Однако это гарантирует, что нет ошибок и данное выражение будет правильно "понято" системойWolframAlpha. Введем это выражение в окошко для обращения к системе и получим правильный ответ.
Пример 6. Сократите дробь: 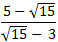 . Вот один из переводов этого задания на язык понятный системе WolframAlpha: (5-sqrt(15))/(sqrt(15)-3). Результат вычислений: 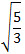 . Пример 7. Упростите выражение: 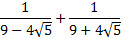 .
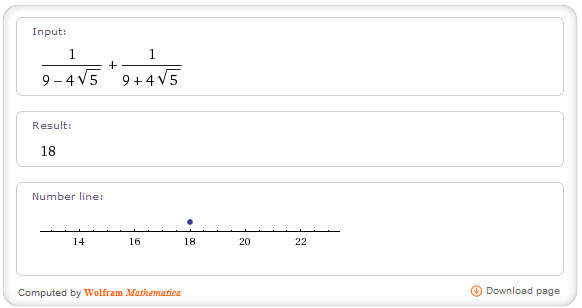
Это задания в системе WolframAlpha запишем так: 1/(9-4*Sqrt[5])+1/(9+4*Sqrt[5]). Однако возможны и другие варианты записи этого выражения. Введя это задание в отведенном окошке а нажав на соответствующую клавишу для начала вычислений мы получим следующий ответ.
В первой строке система WolframAlpha сообщает нам какое выражение она вычисляла, а во второй строке показано значение этого выражения. В том случае когда мы по тем или иным причинам введем данное в задании выражение неверно, можно лего исправить эту ошибку (отредактировать задание).
Пример 8. Вычислите 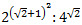 . Ничем не примечательный ст очки зрения математики пример. Однако при его переводе на язык системы WolframAlpha могут возникнуть некоторые трудности. Dвот одна из правильных записей этого задания: 2^((2^(1/2)+1)^2)/(4^(2^(1/2)).
Пример 9. Раскройте модуль: 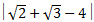 . Вот запись этого задания в системе обозначений, принятой в WolframAlpha: abs(sqrt(2)+sqrt(3)- 4). Далее,как говорится дело техники, т. е. системы
WolframAlpha. Выполните самостоятельный ввод этого задания и посмотрите правильный ответ.
Задачи для самостоятельного решения
1. Выполните действия: 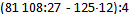 .
2. Вычислите:  .
3. Найдите значение выражения: 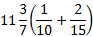 .
4. Сократить дробь 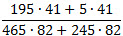 .
5. Вычислить: 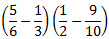 . 6. Вычислите значения выражения: 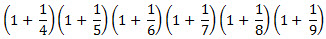 .
7. Найдите значение выражения: 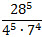 . 8. Найдите значение числового выражения: 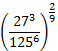 .
9. Вычислите: 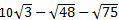 .
10. Вычислите: 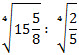 . 11. Вычислите: 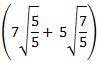 . 12. Упростите выражение:  . 13. Упростите: 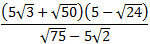 .
| 
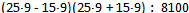 .
.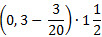 .
.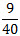 .
.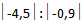
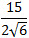 .
.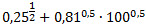 .
.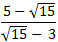 .
.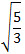 .
.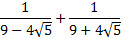 .
.
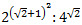 .
.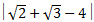 .
.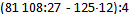 .
. .
.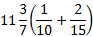 .
.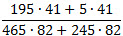 .
.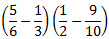 .
.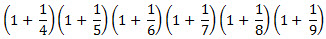 .
.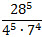 .
.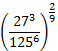 .
.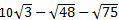 .
.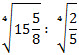 .
. .
. .
. .
.